Concepto de rentabilidad
La rentabilidad es una medida fundamental en el mundo financiero que nos permite evaluar el beneficio obtenido de una inversión en términos relativos.
A menudo, se confunde con el rendimiento, que expresa el beneficio en términos absolutos. ⚠️⚠️
Por ejemplo, si invertimos 20.000 euros y obtenemos un beneficio de 1.000 euros, y otra persona invierte 10.000 euros y obtiene el mismo beneficio, el rendimiento en ambos casos es 1.000 euros, pero la rentabilidad no es la misma:
| Inversión (€) | Beneficio (€) | Rentabilidad (%) |
|---|---|---|
| 20.000 | 1.000 | 5% |
| 10.000 | 1.000 | 10% |
Además, el tiempo en el que se obtiene el beneficio también influye en la rentabilidad.
Una inversión que genera un 5% en un año es menos rentable que otra que genera el mismo 5% en seis meses, ya que al anualizar los resultados, la segunda tendría una rentabilidad mayor.
Rentabilidad Simple
La rentabilidad simple de una inversión se calcula comparando la ganancia o pérdida obtenida (plusvalía o minusvalía) respecto a la inversión inicial. Es una medida básica de rentabilidad que no tiene en cuenta el tiempo que ha transcurrido para obtener esa ganancia o pérdida.
Se expresa mediante la siguiente fórmula:
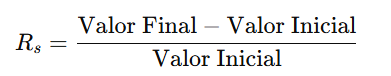
Rentabilidad Nominal
La rentabilidad nominal de una inversión es aquella que se obtiene sin considerar la inflación. Es decir, representa el beneficio financiero en términos brutos.
rentabilidad real
la rentabilidad real tiene en cuenta la pérdida de poder adquisitivo causada por la inflación. Esto es importante porque una rentabilidad nominal elevada puede no ser tan atractiva si los precios aumentan considerablemente en el mismo periodo.
Supongamos que una inversión ofrece una rentabilidad nominal del 6% anual y la inflación en el mismo periodo es del 2%.
Para calcular la rentabilidad real tendremos que dividir 1+ la rentabilidad nominal (0,06) entre 1+ la inflación (0,02), de este modo quedaría así:
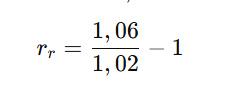
En este caso, aunque la rentabilidad nominal es del 6%, la rentabilidad real, descontando el efecto de la inflación, es del 3,92%.
Esto demuestra que es fundamental analizar la rentabilidad real, para conocer el verdadero crecimiento del poder adquisitivo de nuestra inversión.
Tasa Anual Equivalente (TAE)
La Tasa Anual Equivalente (TAE) es una medida del coste o rendimiento real de un producto financiero, ya sea una inversión o un préstamo. Su cálculo tiene en cuenta la capitalización compuesta de los intereses y, en el caso de los préstamos, también los gastos y comisiones adicionales.
Existen tres medidas principales de tipos de interés en productos financieros:
- Tipo de Interés Nominal (TIN): Es la rentabilidad de un producto financiero en términos anuales, aunque los pagos o desembolsos se realicen en fracciones de año.
- Tipo de Interés Fraccionado: Es el tipo de interés aplicado a cada período de fraccionamiento del año (por ejemplo, semestral, trimestral, mensual, etc.).
- Tasa Anual Equivalente (TAE): Es la rentabilidad efectiva de un producto financiero en un año, suponiendo que no existen gastos adicionales y que los intereses generados se reinvierten según la capitalización compuesta.
La relación matemática entre estos tipos de interés es:
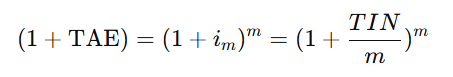
Donde:
- i_m = Tipo de interés fraccionado
- m = Número de fracciones del año
- TIN = Tipo de interés nominal
Importancia de la TAE
El valor de la TAE refleja la naturaleza de la capitalización compuesta, ya que supone una reinversión de los intereses generados.
- Si no hay comisiones ni cargos adicionales, la TAE coincide con el tipo de interés real o efectivo.
- Si existen comisiones u otros gastos financieros, la entidad financiera debe incluirlos en la TAE, según la Circular 5/2012 del Banco de España.
Cálculo de la TAE
Caso 1: Cuenta corriente con pagos semestrales
Supongamos que este producto de ahorro ofrece pagos semestrales a un TIN del 4% anual.
Dado que el interés se paga cada 6 meses, tenemos:
- m = 2 (pagos semestrales en un año).
- TIN = 4% = 0,04.
Aplicamos la fórmula:
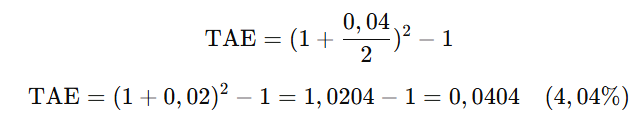
Por lo tanto, la TAE es del 4,04%, ligeramente superior al TIN debido a la capitalización semestral de los intereses.
Caso 2: Préstamo con comisión de apertura
Imaginemos un préstamo simple en el que:
- Se solicita 30.000 euros.
- Se devuelve en un solo pago al cabo de un año.
- Tipo de interés nominal anual (TIN) = 3%.
- Comisión de apertura = 0,5% sobre el capital prestado.
1️⃣La comisión de apertura se calcula como:
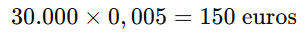
2️⃣Por lo que el capital efectivo recibido es:
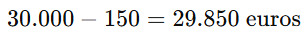
3️⃣Dado que el préstamo tiene un TIN del 3% anual y se devuelve en un solo pago al final del año, el total a devolver es:
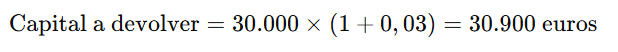
4️⃣ CALCULAR TAE
La TAE mide el coste real del préstamo, teniendo en cuenta tanto los intereses como los gastos adicionales (en este caso, la comisión de apertura). Se calcula con la fórmula:
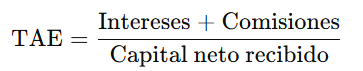
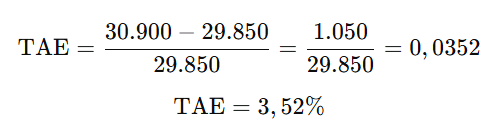
También se podría calcular directamente sumando el total de intereses que serían 900€ + la comisión de apertura que en este caso serían 150€. Esto lo dividiríamos entre el importe neto que nos presta el banco y ya tendríamos calculada la TAE.
Tasa Interna de Rentabilidad (TIR)
La Tasa Interna de Rentabilidad (TIR) es el tipo de interés que hace que el Valor Actual Neto (VAN) de un proyecto sea igual a 0.
En otras palabras, es el rendimiento que una inversión genera internamente sin considerar fuentes de financiación externas.
Cuando realizamos una inversión, esperamos recibir flujos de caja futuros. La TIR nos dice cuál es la rentabilidad anualizada que esa inversión genera, suponiendo que todos los ingresos intermedios se reinvierten a la misma tasa de la TIR.
La TIR se calcula resolviendo la ecuación del VAN:
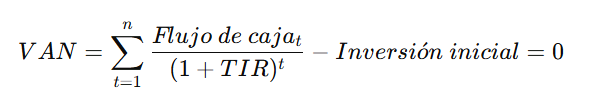
Donde:
- Flujo de caja_t: ingresos o beneficios generados en cada periodo.
- n: número de periodos.
- Inversión inicial: el capital invertido al inicio.
- TIR: tasa de rentabilidad que buscamos.
Ejemplo de Cálculo de la TIR
Supongamos una inversión en renta fija de 7.000 euros con una duración de 20 años. Esta inversión genera cupones anuales del 3% y se adquiere con un descuento del 2% sobre su valor nominal.
Paso 1: Determinar los flujos de caja
- Valor nominal del bono: 7.000€.
- Precio de compra o desembolso inicial (descontado 2%):
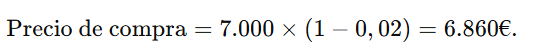
Flujo anual de cupones:
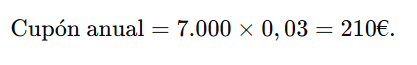
Flujo final (valor nominal al vencimiento): 7.000€.
Paso 2: Aplicar la ecuación del VAN
Buscamos la TIR que satisface la ecuación:
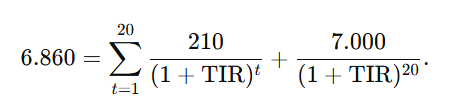
Este tipo de ecuación se resuelve iterativamente, ya que no se puede despejar TIR directamente. Utilizando un método numérico (por ejemplo, Excel o una calculadora financiera), se obtiene:
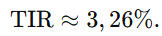
Por lo tanto, la TIR de esta inversión es del 3,26% anual. Es ligeramente mayor que el 3% que dan los bonos, debido a que han sido adquiridos con descuento respecto a su valor nominal.
Tasa de Rentabilidad Efectiva (TRE)
Cuando calculamos la Tasa Interna de Rentabilidad (TIR), asumimos que todos los flujos de caja intermedios (cupones) se reinvierten al mismo tipo de interés. Sin embargo, en la realidad, los tipos de interés pueden variar con el tiempo.
Para obtener una medida más realista de la rentabilidad, usamos la Tasa de Rentabilidad Efectiva (TRE), que tiene en cuenta que los flujos de caja intermedios pueden reinvertirse a tasas de interés diferentes.
calculo rentabilidad efectiva
- Calculamos el valor final de los cupones: Cada cupón recibido se capitaliza hasta el final del periodo con el tipo de interés correspondiente.
- Comparamos el valor final de los cupones con la inversión inicial: El tipo de interés que iguala el valor futuro de los cupones con el valor final de la inversión es la TRE.

Donde:
- T = Número total de años.
- VF_total = Valor final de los flujos de caja.
- Inversión inicial = Precio pagado por la inversión.
Ejemplo TRE
Supongamos que tenemos los siguientes datos:
- Inversión inicial = 6.860€ (se compró con un 2% de descuento sobre el nominal de 7.000€).
- Cupones anuales = 3% de 7.000€ = 210€.
- Valor nominal al final = 7.000€.
- Tasas de reinversión:
- 1º año → 2.5%
- 2º año → 2.7%
- 3º año → 3.5%
- 4º año → 4%.


La Tasa de Rentabilidad Efectiva (TRE) es del 3.41% anual, lo que significa que, considerando la reinversión de los cupones a tasas diferentes, la inversión genera una rentabilidad efectiva mayor que la TIR.
Tasa Geométrica de Rentabilidad (TGR)
La Tasa Geométrica de Rentabilidad (TGR) mide la rentabilidad media anual de una inversión a lo largo de varios períodos, considerando la reinversión de los rendimientos obtenidos. Se diferencia de la rentabilidad simple, ya que tiene en cuenta el efecto de la capitalización compuesta.
Fórmula de la TGR
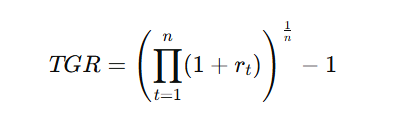
Donde:
- r_t = Rentabilidad obtenida en cada año.
- n = Número de años.
Ejemplo
Supongamos que una inversión tiene las siguientes rentabilidades anuales:
- Año 1: 5% (0.05)
- Año 2: 3% (0.03)
- Año 3: 4% (0.04)
Aplicamos la fórmula:
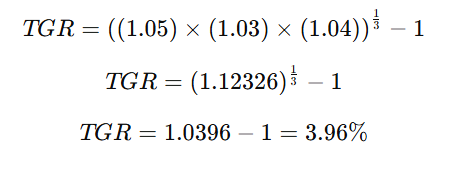
La TGR es del 3.96%, mostrando el efecto de la capitalización de los rendimientos.
